Relaxation Oscillator using Op-amp

An operational amplifier is an integral part of Electronics, and we previously learned about Op-amps in various op-amp-based circuits and also built many oscillator circuits using op-amps and other electronics components.

An oscillator generally refers to the circuit which produces periodic and repetitive output, like a sine wave or square wave. An oscillator can be a mechanical or electronic construction that produces oscillation depending on a few variables. Previously, we learned about many popular oscillators like the RC Phase shift oscillator, the Colpitts oscillator, the Wein bridge oscillator, etc. Today, we will learn about a Relaxation Oscillator.  Among the diverse family of oscillators, the relaxation oscillator using op-amp stands out as a versatile and practical circuit for generating non-sinusoidal waveforms.

What is a Relaxation Oscillator?

A relaxation oscillator is a periodic signal generator that produces non-sinusoidal waveforms, for example, a square wave, triangular wave, or rectangular wave, using passive energy storage elements (for example, capacitors/ inductors) and nonlinear elements such as op-amps or transistors.

A relaxation oscillator satisfies all the conditions below:

• It must provide a non-sinusoidal waveform (of either voltage or current parameter) at the output.
• It must provide a periodic signal or repetitive signal like a Triangular, Square or Rectangular wave at the output.
• The circuit of a relaxation oscillator must be a nonlinear one. That means the design of the circuit must involve semiconductor devices like a Transistor, MOSFET or OP-AMP.
• The circuit design must also involve an energy-storing device like a Capacitor or Inductor, which charges and discharges continuously to produce a cycle. The frequency or period of oscillation for such an oscillator depends on the time constant of its respective capacitive or inductive circuit. 

Relaxation Oscillator Key Characteristics

Characteristic	Description
Output Waveform	Non-sinusoidal (Square, Triangular, Rectangular)
Circuit Type	Nonlinear with semiconductor devices
Energy Storage	Capacitor or Inductor required
Frequency Control	Determined by RC or LC time constant

Working Principle of Relaxation Oscillator

For a better understanding of the relaxation oscillator using op-amp, let us first look into the working of a simple mechanism shown below.

The mechanism shown here is a seesaw that everyone has probably experienced in their life. Plank moves back and forth depending on the gravitational force experienced by the masses on both ends. In simple terms, the seesaw is a comparator of ‘Mass’, and it compares the mass of objects placed on both ends of the plank. So whichever object has a higher mass gets levelled to the ground while the lower mass object is lifted into the air.

In this seesaw setup, we will have a fixed mass ‘M’ on one end and an empty bucket on the other end, as shown in the figure. At this initial state, the mass ’M’ will be levelled to the ground, and the bucket will be hung in the air based on the seesaw principle discussed above.

Now, if I turn on the tap placed above the empty bucket, then the water starts filling the empty bucket and thereby increasing the mass of the entire setup.

And once the bucket gets full, then the entire mass on the bucket side will be more than the fixed mass M placed on the other end. So the plank moves along the axis, thereby airlifting the Mass M and grounding the water bucket.

Once the bucket hits the ground, the water in the bucket gets spilt completely over the ground as shown in the figure. After the spillage, the total mass on the bucket side will again become less compared to the fixed mass M. So again the plank moves along the axis, thereby shifting the bucket to the air again for another filling.

This cycle of filling and spilling keeps on going up until the water source is present to fill the bucket. And because of this cycle, the plank moves along the axis with periodic intervals, thereby giving an oscillation output.

Now, if we compare the mechanical components with the electrical components, then we have.

• The bucket can be considered as an energy-storing device, which is either a capacitor or an inductor.
• Seesaw is a comparator or an op-amp used for comparing the voltages of the capacitor and reference.
• Reference voltage is taken for nominal comparison of the capacitor value.
• The water flow here can be termed as an electric charge.

Mechanical vs Electronic Component Comparison

Mechanical Component	Electronic Equivalent	Function
Water Bucket	Capacitor/Inductor	Energy storage and release
Seesaw/Balance	Op-Amp Comparator	Voltage level comparison
Fixed Mass M	Reference Voltage	Threshold determination
Water Flow	Electric Current	Energy transfer medium

Relaxation Oscillator Circuit Diagram and Design

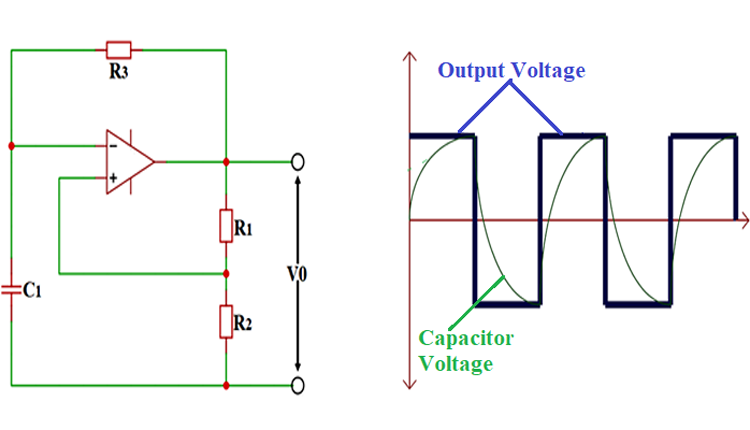
If we draw the equivalent electrical circuit for the above seesaw mechanism, we will get the Relaxation Oscillator Circuit Diagram as shown below:

The relaxation oscillator using op-amp operates through coordinated component interactions. The working of this Op-amp Relaxation Oscillator can be explained as follows:

• Once the tap is turned on, the water flows into a water bucket, thereby filling it slowly.
• After the water bucket is filled, the entire mass on the bucket side will be more than the fixed mass M placed on the other end. Once this happens, the plank shifts its position to a more compromising place.
• After the water is completely spilt out, the total mass on the bucket side will again become less compared to the fixed mass M. So the shaft will move again to its initial position.
• Once again, the bucket gets filled with water after the previous dispel, and this cycle continues forever until there is water flowing from the tap.

If we draw the graph for the above case, it will look something like this:

Here,

• Initially, if we consider that the output of the comparator is high, then during this time, the capacitor will be charging. With the charging of the capacitor, its terminal voltage will gradually rise, which can be seen in the graph.
• Once the capacitor terminal voltage reaches the threshold, the comparator output will go from high to low, as shown in the graph. And when the comparator output goes negative, the capacitor starts discharging to zero. After the capacitor completely discharges because of the presence of a negative output voltage, it again charges, except in the opposite direction. As you can see in the graph, because of the negative output voltage, the capacitor voltage also rises in a negative direction.
• Once the capacitor charges to the maximum in a negative direction, the comparator switches the output from negative to positive. Once the output switches to a positive cycle, the capacitor discharges in the negative path and builds up charges in the positive path as shown in the graph.
• So the cycle of capacitor charge and discharge in positive and negative paths triggers the comparator to produce a square wave signal at the output, which is shown above.

Relaxation Oscillator Frequency Formula and Calculations

The relaxation oscillator frequency formula determines the oscillation rate based on circuit component values. Obviously, the frequency of oscillation depends on the time constant of C1 and R3 in the circuit. Higher values of C1 and R3 will lead to longer charge and discharge rates, thus producing lower frequency oscillations. Similarly, smaller values will produce higher frequency oscillations.

Here, R1 and R2 also play a critical role in determining the frequency of the output waveform. This is because they control the voltage thresholds that the C1 needs to charge up to. For example, if the threshold is set to 5V, then C1 only needs to charge and discharge up to 5V and 5V, respectively. On the other hand, if the threshold is set to 10V, then C1 is needed to charge and discharge to 10V and -10V.

So the Relaxation Oscillator Frequency Formula will be:

f = 1 / 2 x R3 x C1 x ln (1 + k / 1 - k)

Here, K = R2 / R1 + R2

If the resistors R1 and R2 are equal to each other, then

f = 1 / 2.2 x R3 x C1

Applications of Relaxation Oscillator Circuits

Relaxation Oscillator can be used in:

• Signal generators
• Counters
• Memory circuits
• Voltage control oscillators
• Fun circuits
• Oscillators
• Multi-vibrators.

Application Category	Specific Uses	Key Benefits
Signal Generation	Function generators, clock signals, timing references	Stable frequency, clean square waves
Digital Circuits	Counters, memory circuits, flip-flop triggers	Compatible logic levels, precise timing
Control Systems	Voltage-controlled oscillators, PWM generation	Voltage-dependent frequency control
Entertainment	Electronic music, sound effects, fun circuits	Audio frequency range, simple construction

Conclusion

The relaxation oscillator using op-amp represents an important basic component in a basic electronic circuit design, generating reliable non-sinusoidal waveforms with simple components. Further, engineers can incorporate knowledge of the relaxation oscillator circuit diagram, frequency formula, and functioning principles to be able to efficiently develop timing and signal generators for several applications.

Frequently Asked Questions on the Relaxation Oscillator Circuit

⇥ 1. What is the difference between a relaxation oscillator and a sinusoidal oscillator?
Relaxation oscillators produce non-sinusoidal waveforms (triangular, square) with nonlinear switching elements, while sinusoidal oscillators produce pure sine waves with linear amplification and selective feedback networks. Relaxation oscillators are more stable and simpler.

⇥ 2. What are the components of a typical relaxation oscillator circuit? 
The components are a comparator (an operational amplifier), timing resistor R₃, timing capacitor C₁ and feedback resistors R₁, R₂. The switching action is provided by the op-amp, and the frequency of the oscillator is controlled by the charge/discharge time of the RC components.

⇥ 3. Why do relaxation oscillators need positive feedback? 
Positive feedback through the R1-R2 network provides hysteresis for rapid switching of the output states and prevents oscillation at threshold values. Without feedback, there would be set upper and lower stable switching thresholds for smooth operation.

⇥ 4. Is the frequency of a relaxation oscillator voltage-controlled? 
Yes, the substitution of the fixed resistor R3 with a voltage-controlled impedance, such as a JFET or OTA (operational transconductance amplifier), is a way to achieve this. Your input control voltage could effectively change resistance, change the RC time constant and provide a proportionate change in oscillation frequency for VCOs.

⇥ 5. What are the primary factors that influence the frequency stability of a relaxation oscillator? 
The major factors are: the temperature coefficient of the components, variations in the power supply, tolerances in resistor values, capacitor leakage, and loading effects. With the use of precision components, regulated power supplies and good design practices, frequency stability can typically be accomplished over time.

⇥ 6. How do you alter the duty cycle of a relaxation oscillator? 
Change the ratio R₁  /R₂ to make the threshold voltage asymmetrical. The asymmetrical thresholds would yield differing charge/discharge times, or you could use completely separate charge/discharge paths with two different RC time constants for precise duty cycle control.

Explore Related Op-Amp Projects

Previously, we have used an Op-amp to build many interesting projects. If you'd like to know more about those topics, I've included links below.