What is Oscillator?
An oscillator is a mechanical or electronic construction which produces oscillation depending on few variables. We all have devices which need oscillators, traditional clock that we all have in our home as a wall clock or wristwatch, various type of metal detectors, computers where microcontroller and microprocessors are involved all use oscillators, especially electronics oscillator which produces periodic signals. There are many types of Oscillators based on there configuration like Hartley Oscillator, Colpitts Oscillator, Wein Bridge Oscillator, Quartz Crystal Oscillator, Phase Shift Oscillator Circuit etc.
RC Oscillator and Phase:
As we discuss about RC oscillator, and as it is also referred as phase shift oscillator we need a fair understanding about what is phase. See this image:-
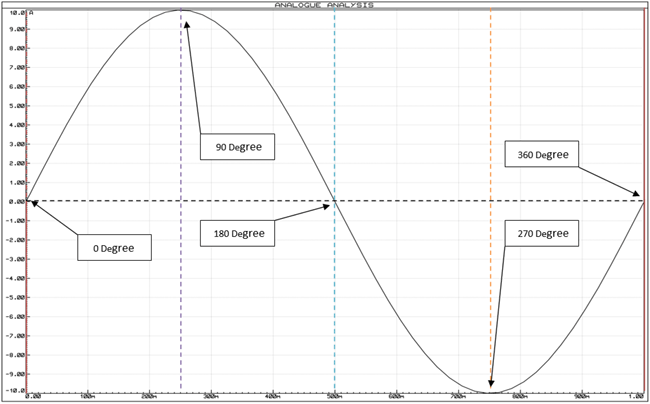
If we see the above sinusoidal wave like this one we will clearly see that the signal’s starting point is 0 degree in phase, and after that every peak point of the signal from positive to 0 then again negative point then again 0 is respectively denotes as 90 degree, 180 degree, 270 degree and 360 degree in phase position.
Phase is a full cycle period of a sinusoidal wave in a 360 degree reference.
Now without further delay let’s see what phase shift is?
If we shift the sinusoidal wave starting point other than the 0 degree the phase is shifted. We will understand phase shift in the next image.
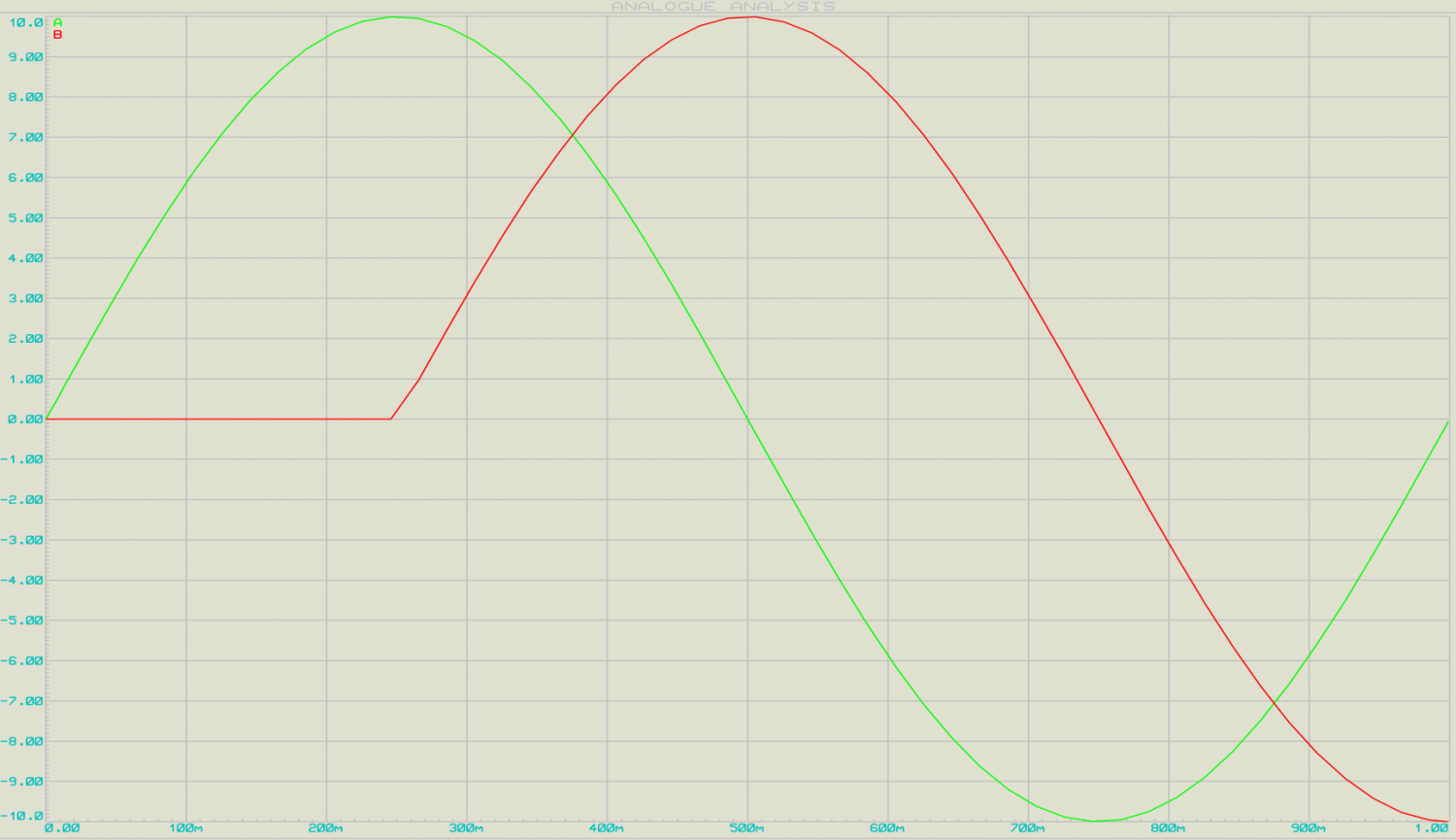
In this image, there are two AC sinusoidal signal wave presented, the first Green Sinusoidal wave is 360 degree in phase but the red one that is the replica of the first, read signal is 90 degree out of the green signal’s phase.
Using RC oscillator we can shift the phase of a Sinusoidal signal.
Phase Shift using RC Oscillator Circuit:
RC stands for Resistor and Capacitor. We can simply form a Phase shift Resistor-capacitor network using just only one resistor and one capacitor formation.
As seen in the High pass filter tutorial, the same circuit applies here. A typical RC phase shift oscillator can be produce by a capacitor in series along with a resistor in parallel.
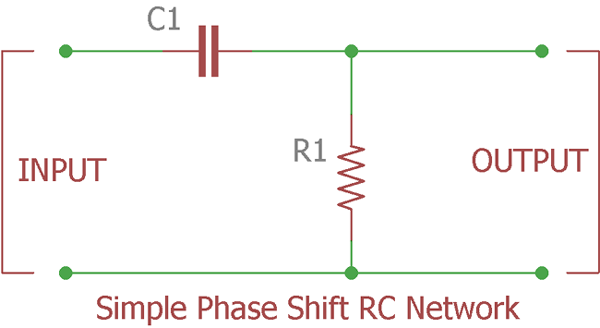
This is a single pole phase shift network; the circuit is same as Passive High Pass Filter. Theoretically if we apply an in phase signal across this RC network the output phase will be shifted by exactly 90 degree. But if we try it in reality and check the phase shift, then we achieve 60 degree to less than 90 degree phase shift. It’s depends on the frequency, and the components tolerances which create adverse effect in reality. As we all know nothing is perfect, there should be some difference than actual so called or expected values than the reality. Temperature and other outer dependencies creates difficulties to achieve exact 90 degree phase shift, 45 degree is in general, 60 degree is common depending on the frequencies and achieving 90 degree is a very difficult job in many cases.
As discussed in High pass tutorial we will construct the same circuit and will investigate about the phase shift of the same circuit.
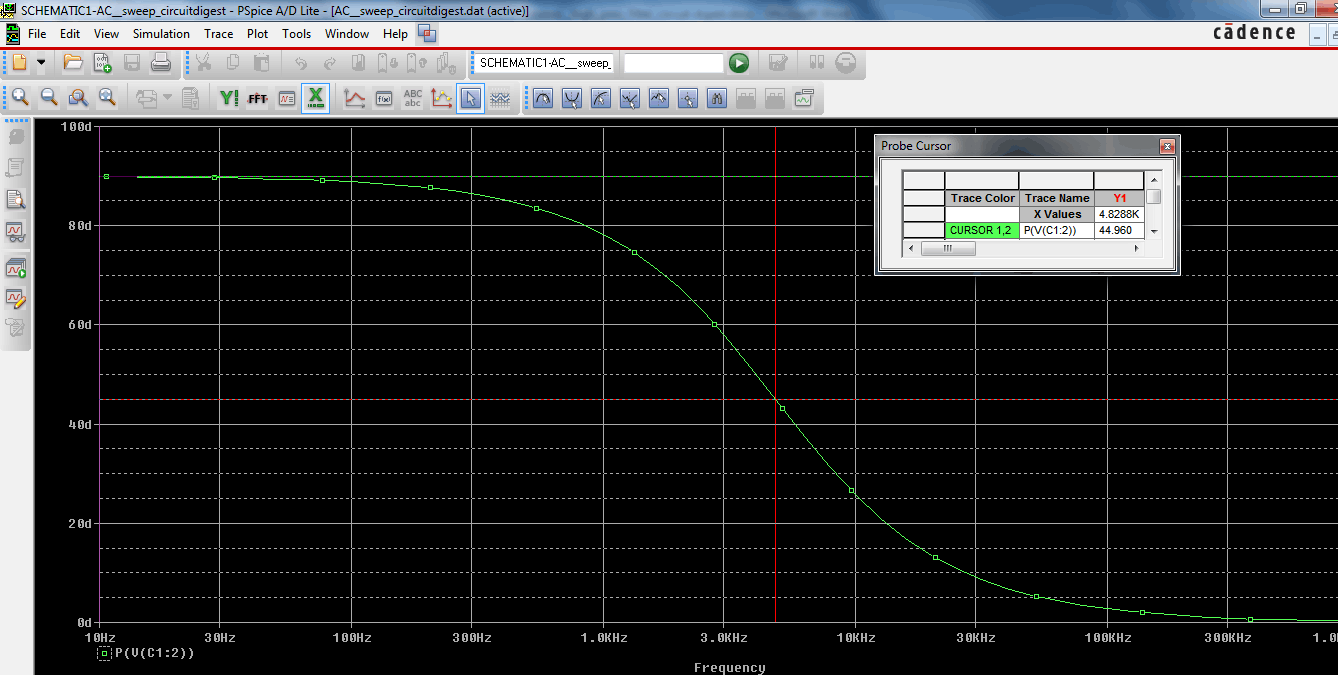
The circuit of that High Pass filter along with the component values is in the below image:-

This is the example we used in previous passive high pass filter tutorials. It will produce 4.9 KHz of Bandwidth. If we check the corner frequency we will identify the phase angle at the output of the Oscillator.
Now we can see the phase shift is started from 90 degree which is the maximum phase shift by RC oscillator network but at the point of corner frequency the phase shift is 45degree.
Now considering the fact that the phase shift is 90 degree or if we select the oscillator circuitry construction like a special way that will produce 90 degree phase shift then the circuit will lose its immunity in border range due to poor frequency stabilization factor. As we can imagine at the point of 90 degree where the curve just started like from the 10Hz or Lower to the 100Hz is almost flat. That means if the oscillator’s frequency changed slightly due to components tolerance, Temperature, other unavoidable circumstances, the phase shift will not change. That is not a good choice. So we consider 60degree or 45 degree is the acceptable phase shift for single pole RC network oscillator. The Frequency stability will improve.
Cascading Multiple RC Filters:
Cascade Three RC Filters:
By considering this fact that we cannot achieve only achieve 60 Degree phase shift instead of 90 degree, we can cascade three RC filters (If the phase shift is 60 degree by RC oscillators) or by cascading four filters in series (If the phase shift is 45 degree by each RC oscillators) and get 180 degree.
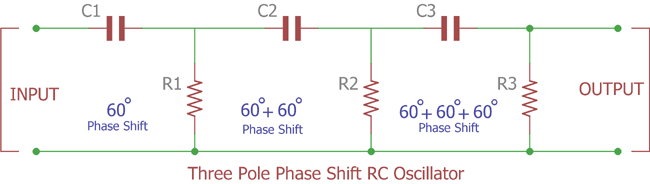
In this image three RC oscillators cascaded and each time 60 degree phase shift added and finally after third stage we will get 180 degree phase shift.
We will construct this circuitry in simulation software and see the input and output wave form of the circuitry.
Before getting into the video lets’ see the image of the circuitry and will see the oscilloscope connection as well.

In the upper image we used 100pF capacitor and 330k resistor value. The oscilloscope is connected across the Input VSIN (A / Yellow channel), across first pole output (B / Blue channel), 2nd pole output
(C / Red channel) and the final output across third pole (D / Green channel).
We will see the simulation in the Video and will see the phase change in 60 degree across first pole, 120degree across second pole and 180 degree across third pole. Also the amplitude of the signal will minimize step by step.
1st pole amplitude > 2nd pole amplitude > 3rd pole amplitude. More we go towards last pole the decrement of amplitude of the signal is decrease.
Now we will see the simulation video:-
It is clearly shown that every pole actively changing the phase shifts and at the final output it is shifted to 180 degrees.
Cascade Four RC Filters:
In the next image four RC phase shift oscillator used with 45-degree phase shift each, which produce 180-degree phase shift at the end of the RC network.

RC Phase Shift Oscillator using Transistor:
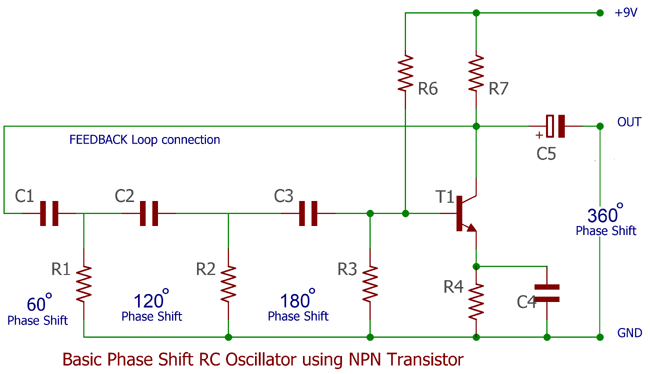
This is all are passive elements or components in the RC oscillator. We get the phase shift of 180 degree. If we want to make a 360 degree phase shift then an active component required which produce additional 180 degree phase shift. This is done by a Transistor or an Amplifier and requires additional supply voltage. Below circuit shows the RC phase shift oscillator using BJT. You can find the practical implementation of Phase Shift Oscillator Circuit here.

In this image a NPN Transistor is used to produce Phase shift of 180 degree while the C1R1 C2R2 C3R3 will produce 60 degree of phase delay. So accumulating this three 60 + 60 + 60 = 180 degree phase shift is done on the other hand adding another 180 degree by the transistor total 360 degree phase shift is created. We will get 360 degree of phase shift across the C5 electrolytic capacitor. If we want to change the frequency of this one way to change the capacitors value or use a variable preset capacitor across those three poles individually by eliminating individual fixed capacitors.
A feedback connection is made to retrieve the energies back to the amplifier using that three pole RC network. It’s necessary for stable positive oscillation and to produce sinusoidal voltage. Due to the feedback connection or the configuration, RC oscillator is a feedback type oscillator.
In 1921, German physicist Heinrich Georg Barkhausen introduced “Barkhausen criterion” for determining the relation between phase shifts across feedback loop. As per the criterion, the circuit will only oscillate if the phase shift around the feedback loop is equal or multiple of 360 degrees and the gain of the loop is equal to one. If the phase shift is accurate at the desired frequency and the feedback loop creates 360-degree oscillation then the output will be a sine wave. RC filter serves to achieve this purpose.
Frequency of RC Phase Shift Oscillator:
We can easily determine the frequency of the Phase Shift Oscillator Circuit:-

Where,
R = Resistance (Ohms)
C = Capacitance
N = Number of RC network is / will be use
This Formula is used for High pass filter related design, we can also use low pass filter and the phase shift will be negative. In such case the upper formula will not work for calculating the frequency of the oscillator, different formula will be applicable.

Where,
R = Resistance (Ohms)
C = Capacitance
N = Number of RC network is / will be use
RC Phase Shift Oscillator using Op-amp:
As we can construct RC phase shift oscillator using Transistor i.e. BJT, there are other limitations of RC phase shift oscillator using BJT.
- It is stable for low frequencies.
- Just using only one BJT the Output wave’s amplitude is not perfect, it is required additional circuitry to stabilized amplitude of the waveform.
- Frequency accuracy is not perfect and it is not immune to noisy interference.
- Adverse Loading effect. Due to cascade formation the second pole’s input impedance change the resistors resistance properties of the first pole filter. More the filters cascaded more the situation worsen up as it will affect the accuracy of calculated phase shift oscillator frequency.
Due to the attenuation across resistor and capacitor, the loss across each stage is increased and the total loss is approx total loss of 1/29th of the input signal.
As the circuit attenuates at 1/29th we need to recover the loss.
This is the time to change the BJT with an Op-amp. We can also recover that four drawbacks and get more headroom over the control if we use op-amp instead BJT. Due to high input impedance the loading effect also effectively controlled because op-amp input impedance promotes to the overall loading effect.
Now without the further modification let’s change the BJT with an Op-Amp and see what will be the circuitry or schematic of the RC oscillator using Op-amp.

As we can see, Just BJT replaced with an inverted op-amp. The Feedback loop is connected across first pole RC oscillator and feed to the op-amp inverted input pin. Due to this inverted feedback connection, the op-amp will produce a 180-degree phase shift. Additional 180-degree phase shift will be provided by the three RC stages. We will get the desired output of 360-degree phase shifted wave across the op-amp first pin named as OSC out. The R4 is used for the gain compensation of the op-amp. We can tweak the circuitry to get high frequency oscillated output but depending on the frequency range bandwidth of the op-amp.
Also, for getting the desired result we need to calculate the gain resistor R4 to achieve 29th times greater amplitude across op-amp as we need to compensate with the loss of 1/29th across RC stages.
Let’s see, we will make a circuit with real components value and see what will be the simulated output of the RC phase shift oscillator.
We will use 10k ohms resistor and 500pF capacitor and determine the frequency of the oscillation. We will also calculate the value of gain resistor.

N= 3, as 3 stages will be used.
R = 10000, as 10k ohms converted to ohms
C = 500 x 10-12 as capacitor value is 500pF

The Output is 12995Hz or the relatively close value is 13 KHz.
As the op-amp gain is needed 29th times the value of the gain resistor is calculated using this formula:-
Gain = Rf / R 29 = Rf / 10k Rf = 290k
This is how Phase shift oscillator is constructed using RC components and Op-amp. You can learn more about RC phase shift oscillator using op amp by following the link.
Applications of RC phase shift oscillator includes amplifiers where the audio transformer is used and differential audio signal needed but the inverted signal is not available, or if AC signal source needed for any application then RC filter are used. Also, signal generator or function generator use RC phase shift oscillator.