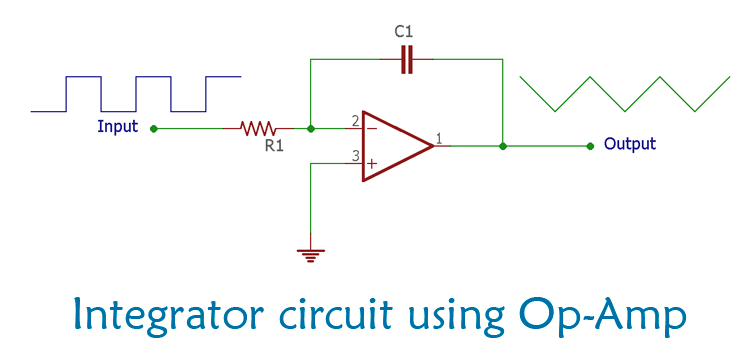
Op-amp or Operational Amplifier is the backbone of Analog Electronics and out of many applications, such as Summing Amplifier, differential amplifier, Instrumentation Amplifier, Op-Amp can also be used as integrator which is a very useful circuit in analog related application.
In simple Op-Amp applications, the output is proportional to the input amplitude. But when op-amp is configured as an integrator, the duration of the input signal is also considered. Therefore, an op-amp based integrator can perform mathematical integration with respect to time. The integrator produces an output voltage across the op-amp, which is directly proportional to the integral of the input voltage; therefore the output is dependent on the input voltage over a period of time.
Construction and Working of Op-amp Integrator Circuit
Op-amp is very widely used component in Electronics and is used to build many useful amplifier circuits.

The construction of simple Integrator circuit using op-amp requires two passive components and one active component. The two passive components are resistor and capacitor. The Resistor and the Capacitor form a first-order low pass filter across the active component Op-Amp. Integrator circuit is exactly opposite of Op-amp differentiator circuit.
A simple Op-amp configuration consists of two resistors, which creates a feedback path. In the case of Integrator amplifier, the feedback resistor is changed with a capacitor.
In the above image, a basic integrator circuit is shown with three simple components. The resistor R1 and capacitor C1 is connected across the amplifier. The amplifier is in Inverting configuration.
Op-amp gain is Infinite, therefore the Inverting input of the amplifier is a virtual ground. When a voltage is applied across the R1, the current start to flow through the resistor as the capacitor has very low resistance. The capacitor is connected in the feedback position and the resistance of the capacitor is insignificant.
At this situation, if the amplifier gain ratio is calculated, the result will be less than the unity. This is because the gain ratio, XC/R1 is too small. Practically, the capacitor has very low resistance between the plates and whatever the value R1 holds, the output result of XC/R1 will be very low.
The capacitor begins to charge up by the input voltage and in the same ratio, the capacitor impedance also starts to increase. The charging rate is determined by the RC - time constant of R1 and C1. The op-amp virtual earth now hampered and the negative feedback will produce an output voltage across the op-amp to maintain the virtual earth condition across the input.
The Op-amp produce a ramp output till the capacitor gets fully charged. The capacitor charges current decreases by the influence of the potential difference between the Virtual earth and the negative output.
Calculating the Output Voltage of Op-amp Integrator Circuit

Let’s see the above image. The iR1 is the current flowing through the resistor. The G is the virtual ground. The Ic1 is the current flowing through the capacitor.
If Kirchhoff’s current law is applied across the junction G, which is a virtual ground, the iR1 will be the sum of current entering in the Inverting terminal (Op-amp pin 2) and the current passing through the Capacitor C1.
iR1 = iinverting terminal + iC1
Since the op-amp is an ideal op-amp and the G node is a virtual ground, no current is flowing through the op-amp’s inverting terminal. Therefore, iinverting terminal = 0
iR1 = iC1
The capacitor C1 has a voltage-current relationship. The formula is –
IC = C (dVC /dt)
Now let's apply this formula in a practical scenario. The  is –
is –
(Vin - VG / R1), where VG is the voltage in virtual ground node
Now the is equal to
C (d(VC – Vout) /dt)
As the G node is a virtual ground point and the op-amp is an ideal op-amp, the voltage across this node is 0.
Therefore,

The basic Integrator circuit, which is shown previously, has a drawback. The capacitor blocks the DC and due to this, the DC gain of the Op-Amp circuit become Infinite. Therefore, any DC voltage at the Op-amp Input, saturates the Op-amp output. To overcome this problem, resistance can be added in parallel with the capacitor. The resistor limits the DC gain of the circuit.
The Op-Amp in Integrator configuration provides different output in a different type of changing input signal. The output behavior of an Integrator amplifier is different in each case of Sine wave input, square wave input or triangular wave input.
Op-amp Integrator Behavior on Square Wave input
If the square wave is provided as an input to Integrator Amplifier, the produced output will be a triangular wave or saw tooth wave. In such a case, the circuit is called a Ramp generator. In square wave, voltage levels change from Low to High or high to low, which makes the capacitor gets charged or discharged.

During the positive peak of the square wave, the current start to flow through the resistor and in the next stage, the current flow through the capacitor. Since the current flow through the op-amp is zero, the capacitor gets charged. The reverse thing will happen during the negative peak of the square wave input. For a high frequency, the capacitor gets very minimal time to fully charge up.
The charging and discharging rate depend on the resistor-capacitor combination. For perfect integration, the frequency or the periodic time of the input square wave needs to be less than the circuit time constant, which is referred as: T should be less than or equal to the CR (T <=CR).
Square wave generator circuit can be used to produce square waves.
Op-amp Integrator Behavior on Sine Wave input
If the input across an op-amp based Integrator circuit is a sine wave, the Op-amp in integrator configuration produces a 90 degree out of phase sine wave across the output. This is called a cosine wave. During this situation, when the input is a sine wave, the integrator circuit acts as an active low pass filter.
As discussed previously, that in low frequency or in DC, the capacitor produces a blocking current which eventually reduces the feedback and the output voltage saturates. In such a case, a resistor is connected in parallel with capacitor. This added resistor provides a feedback path.

In the above image, an additional resistor R2 is connected in parallel with the capacitor C1. The output sine wave is 90 degree out of phase.
The corner frequency of the circuit will be
Fc = 1 / 2πCR2
And the overall DC gain can be calculated using –
Gain = -R2 / R1
Sine wave generator circuit can be used to generate sine waves for integrator input.
Op-amp Integrator Behavior on Triangular Wave input

In triangular wave input, the op-amp again produces a sinusoidal wave. As the amplifier act as a low pass filter, the high-frequency harmonics are greatly reduced. The output sine wave only consists of low-frequency harmonics and the output will of low amplitude.
Applications of Op-amp Integrator
- Integrator is an important part of the instrumentation and is used in Ramp generation.
- In function generator, the integrator circuit is used to produce the triangular wave.
- Integrator is used in wave shaping circuit such as a different kind of charge amplifier.
- It is used in analog computers, where integration is needed to be done using the analog circuit.
- Integrator circuit is also widely used in analog to the digital converter.
- Different sensors also use an integrator to reproduce useful outputs.





