Active Low Pass Filter

Previously we described passive low pass filter, in this tutorial we will explore what is an Active Low Pass Filter.

What is it, Circuit, formulas, curve?

As we know from previous tutorial, Passive low pass filter works with passive components. Only two passive components resistor and capacitor is the key or heart of a passive low pass filter circuit. We learned in the previous tutorials that passive low pass filter work’s without any outer interruption or active response. But it has certain limitations.

 

Limitations of Passive Low pass filter are as follows:-

1. The impedance of the circuit creates loss of the amplitude. So the Vout is always less than the Vin.
2. Amplification cannot be done with only passive low pass filter.
3. Filter characteristics are greatly dependable on the load impedance.
4. The gain is always equal or lesser than the unity gain.
5. More the filter stages or filter order added the loss of amplitude become lesser.

Due to this limitation, if Amplification needed, the best way to add an active component which will amplify the filtered output. This Amplification is done by operational amplifier or op-amp. As this requires voltage source, it’s an active component. Thus the name Active low pass filter.

A typical Amplifier draws the power from the external power supply and amplifies the signal but it is highly flexible as we can change the frequency bandwidth more flexibly. Also, It is user’s or the designer’s choice to select what type of active components to choose depending on the requirements. It can be Fet, Jfet, Transistor, Op-Amp which include a lot of flexibility. The choice of component is also dependable on the cost and the effectiveness if it is designed for a mass production product.

For the sake of simplicity, time effectiveness and also the growing technologies in op-amp design, generally an op-amp is used for Active Filter design.

 

Let’s see why we should choose and op-amp to design an Active low pass filter:-

1. High input impedance.
   Due to high input impedance the input signal couldn’t be destroyed or altered. In general or in most cases the input signal which is a very low in amplitude could be destroyed if it is used as low impedance circuitry. Op-Amp got a plus point in such cases.
2. Very low component count. Only few resistors are needed.
3. Various type of op-amp is available depending on the gain, voltage specification.
4. Low noise.
5. Easier to design and implementation.

But as we know nothing is entirely perfect, this Active filter design also have certain limitation.
The output gain and bandwidth as well as frequency response are dependable on the op-amp specification.

Let’s Explore further and understand what is special about it.

 

Active Low Pass Filter with Amplification:

Before understanding Active low pass filter design with op-amp, we need to know a little bit about Amplifiers. Amplify is a magnifying glass, it produces a replica of what we see but in bigger form to recognize it better.

In the first tutorial of Passive low pass filter, we had learned what was Low Pass filter. Low pass filter filtered out low frequency and block higher one of an AC sinusoidal signal. This Active low pass filter is work in the same way as Passive low pass filter, only difference is here one extra component is added, it is an amplifier as op-amp.

Here is the simple Low pass filter design:-

This is the image of Active low pass filter. Here the violate line shows us the traditional passive low pass RC filter we seen in previous tutorial.

 

Cut off Frequency and Voltage gain:

The Cut off frequency formula is same as used in passive low pass filter.

fc = 1 / 2πRC

As described in previous tutorial fc is cut-off frequency and the R is Resistor value and the C is Capacitor value.

The two resistor connected in the positive node of the op-amp are feedback resistors. When these resistors are connected in positive node of the op-amp it is called non-inverting configuration. These resistors are responsible for the amplification or the gain.

Amplifier Gain (DC amplitude)(Af) = (1+R2/R3)

Frequency Response Curve:

Let’s see what will be the output of the Active Low pass filter or the Bode plot/Frequency response curve:-

This is the final output of Active Low pass filter in op-amp non-inverting configuration. We will see in detail explanation in next image.

As we see this is identical with Passive low pass filter. From the starting frequency to the Fc or frequency cut-off point or the corner frequency will start from -3dB point. The gain is 20dB in this image, so the cut-off frequency is 20dB - 3dB = 17dB where the fc point is situated. The slope is -20dB per decade.

Irrespective of the filter, from the starting point to the cut-off frequency point it is called Bandwidth of the filter and after that, it is called pass band from which the passing frequency is allowed.

We can calculate the magnitude gain by converting the op-amp Voltage gain.

The calculation is as follows

db = 20log(Af)

This Af can be the Dc gain we described before by calculating the resistor value or dividing the Vout with Vin.

 

Non-inverting and Inverting Amplifier Filter Circuit:

This active low pass filter circuit shown in the beginning also has one limitation. Its stability can be compromised if the signal source impedance changed. E.g. decrease or increase.

A standard design practice could improve the stability, removing the capacitor from input and connecting it parallel with op-amp second feedback resistor.

Here is the circuit Non-inverting Active Low pass Filter-

In this figure, if we compare this with the circuitry described in the beginning, we can see that the capacitor position is altered for impedance related stability. In this configuration the external impedance makes no effect on the capacitors reactance, thus the stability improved.

On the same configuration if we want to invert the output signal then we can choose the inverting-signal configuration of the op-amp and could connect the filter with that inverted op-amp.

 

Here is the circuitry implementation of inverted active low pass filter:-

It is an active low pass filter in inverted configuration. The op-amp is connected inversely. In the previous section the input was connected across op-amp’s positive input pin and the op-amp negative pin is used to make the feedback circuitry. Here the circuitry inverted. Positive input connected with ground reference and the capacitor and feedback resistor connected across op-amp negative input pin. This is called inverted op-amp configuration and the output signal will be inverted than the input signal.

 

Unity Gain or Voltage Follower Active Low Pass Filter:

Till now the circuitry described here is used for voltage gain and post-amplification purpose.

We can make it using a unity gain amplifier, that means the output amplitude or gain will be same as input: 1x. Vin = Vout.

Not to mention, it is also an op-amp configuration which often described as voltage follower configuration where the op-amp created the exact replica of the input signal.

Let’s see the circuit design and how to configure the op-amp as voltage follower and make the unity gain active low pass filter:-

In this image, the feedback resistors of the op-amp are removed. Instead of the resistor the negative input pin of the op-amp connected directly with the output op-amp. This op-amp configuration is called as Voltage follower configuration. The gain is 1x. It is a unity gain active low pass filter. It will produce exact replica of the input signal.

 

Practical example with Calculation

We will design a circuitry of active low pass filter in non-inverting op-amp configuration.

Specifications:-

1. Input Impedance 10kohms
2. Gain will be 10x
3. Cutoff freq will be 320Hz

 

Let’s calculate the value first before making the circuitry:-

Amplifier Gain (DC amplitude)(Af) = (1+R3/R2) 
(Af) = (1+R3/R2) 
Af = 10

R2= 1k (We need to select one value; we selected R2 as 1k for reducing the complexity of the calculation).

By putting the value together we get

(10) = (1+R3/1) 

We calculated the value of the third resistor is 9k.

Now we need to calculate the value of the resistor according to the cut-off frequency. As active low pass filter and the passive low pass filter works on the same way the frequency cut-off formula is same as before.

Let’s check the value of the capacitor if the cut-off frequency is 320Hz, we selected the value of the resistor is 4.7k.

fc = 1 / 2πRC

 By putting all value together we get:-

By solving this equitation we get the value of the capacitor is 106nF approximately.

Next step is to calculate gain. The formula of the gain is same as passive low pass filter. The formula of gain or magnitude in dB is as follows:-

20log(Af)

As the gain of the op-amp is 10x the magnitude in dB is 20log(10). This is 20dB.

 

Now as we already calculated the values now it is the time to construct the circuit. Let’s add all together and build the circuit:-

We constructed the circuit based on the values calculated before. We will provide 10Hz to 1500Hz frequency and 10 points per decade at the input of the active low pass filter and will investigate further to see whether the cutoff frequency is 320Hz or not at the output of the amplifier.

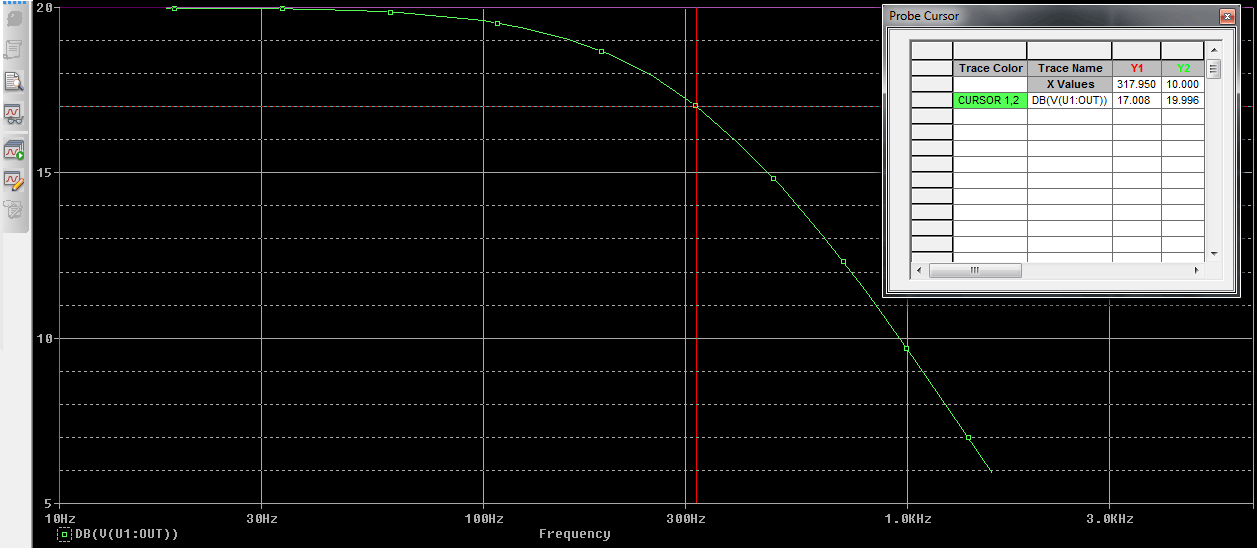
This is the frequency response curve. The green line is started from 10Hz to 1500Hz as the input signal is supplied for that range of frequency only.

As we know that the corner frequency will be always at -3dB from the Maximum gain magnitude. Here the gain is 20dB. So, if we find out the -3dB point will get the exact frequency where the filter stops the higher frequencies.

We set the cursor at the 17 db as (20dB-3dB = 17dB) the corner frequency and get 317.950Hz or 318Hz which is close to the 320Hz.

We can change the capacitor value to the generic one as 100nF and not mention the corner frequency will also effected by few Hz.

 

Second Order Active Low Pass Filter:

It’s possible to add more filters across one op-amp like second order active low pass filter. In such case just like the passive filter, extra RC filter is added.

Let’s see how the second order filter circuit is constructed.

This is the Second order filter. In the above figure we can clearly see the two filters added together. This is the second order filter.  It is a widely used filter and industrial application is Amplifier, Musical system circuitry before the Power Amplification.

As you can see there is one op-amp. The voltage gain is same as previously stated using two resistors.

(Af) = (1+R3/R2) 

The cut-off frequency is

One interesting thing to remember if we want to add more op-amp which consist first order filters the gain will be multiplied by each individual. Confused? May be a schematic will help us.

The more the op-amp added the more gain is multiplied. See the above figure, In this image two op-amp cascaded with individual op-amp. In this circuit the Cascaded op amp, If the first one is having 10x gain and the second one is for 5x gain then the total gain will be 5 x 10 = 50x gain.

So, the magnitude of the cascaded op-amp low pass filter circuit in case of two op-amp is:-

dB = 20log(50)

By solving this equation it is 34dB. So the gain of cascading op-amp low pass filter gain formula is

 TdB = 20log(Af1*Af2*Af3*......Afn)

Where TdB = Total Magnitude
 

This is how Active low pass filter is constructed. On the next tutorial, we will see how Active high pass filter can be constructed. But before the next tutorial let’s see what the applications of Active low pass filter are:-

 

Applications

Active Low pass filter can be used at multiple places where passive low pass filter cannot be used due to the limitation about gain or amplification procedure. Apart from that the active low pass filter can be used in following places:-

Low pass filter is widely used circuit in electronics.

Here are few applications of Active Low Pass Filter:-

1. Bass equalization before Power amplification
2. Video related filters.
3. Oscilloscope
4. Music control system and Bass frequency modulation as well as before woofer and high bass audio speakers for bass out.
5. Function Generator to provide variable low frequency out at different voltage level.
6. Changing the frequency shape at different wave from.