In previous tutorial of half adder circuit construction, we had seen how computer uses single bit binary numbers 0 and 1 for addition and create SUM and Carry out. Today we will learn about the construction of Full-Adder Circuit.
Here is a brief idea about Binary adders. Mainly there are two types of Adder: Half Adder and Full Adder. In half adder we can add 2-bit binary numbers but we cant add carry bit in half adder along with the two binary numbers. But in Full Adder Circuit we can add carry in bit along with the two binary numbers. We can also add multiple bits binary numbers by cascading the full adder circuits which we will see later in this tutorial. We also use IC 74LS283N to practically demonstrate the Full Adder circuit.
Difference between Half Adder and Full Adder
Before getting to the details about the full adder let's see what the main differences between the half adder and the full adder are.
| Feature | Half Adder | Full Adder |
| Number of Inputs | 2 (A, B) | 3 (A, B, Cin) |
| Input Type | Two 1-bit binary numbers | Two 1-bit binary numbers and a carry-in bit |
| Functionality | Adds two binary digits | Adds two binary digits and considers the carry from the previous addition. |
| Outputs | Sum (S) and Carry (C) | Sum (S) and Carry-out (Cout) |
| Carry Handling | Ignores carry from the previous addition. | Includes carry from the previous addition. |
| Complexity | Simpler design | More complex design |
| Applications | Limited (used as the building block for full adders) | Multi-bit addition, digital processors |
Full Adder Circuit:
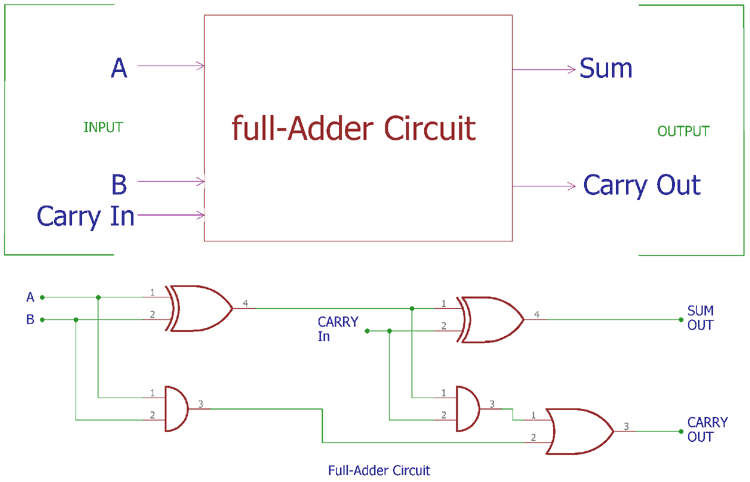
So, we know that Half-adder circuit has a major drawback that we do not have the scope to provide ‘Carry in’ bit for addition. In case full adder construction, we can actually make a carry in input in the circuitry and could add it with other two inputs A and B. So, in the case of Full Adder Circuit we have three inputs A, B and Carry In and we will get final output SUM and Carry out. So, A + B + CARRY IN = SUM and CARRY OUT.

The above image shows the typical logic diagram of a full adder. As you can it can accept 3 pinouts including a carry in and can provide two outputs including sun and carry out. As per mathematics, if we add two half numbers we would get a full number, the same thing is happening here in full adder circuit construction. We add two half-adder circuits with an extra addition of OR gate and get a complete full adder circuit.
Implementation of Full Adder using Half Adder
Let’s see the block diagram,

The above block diagram shows a Full adder circuit construction, where two half adder circuits are added together with an OR gate. The first half adder circuit is on the left side, we give two single-bit binary inputs A and B. As seen in the previous half adder tutorial, it will produce two outputs, SUM and Carry out. The first half adder circuit’s SUM output is further provided to the second half adder circuit’s one input along with the carry in bit across the other input. Again, it will provide SUM out and carry out bit. This SUM output is the final output of the Full adder circuit. On the other hand, the Carry out of the first half adder circuit and the Carry out of the second adder circuit is further provided into the OR logic gate. After the logic OR of two Carry outputs, we get the final carry out of the full adder circuit.
The Final Carry out represents the most significant bit or MSB.
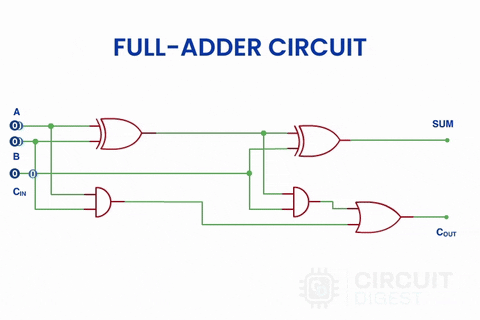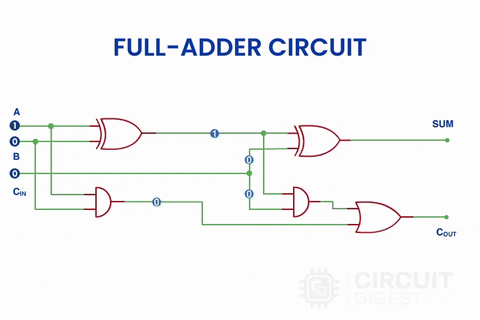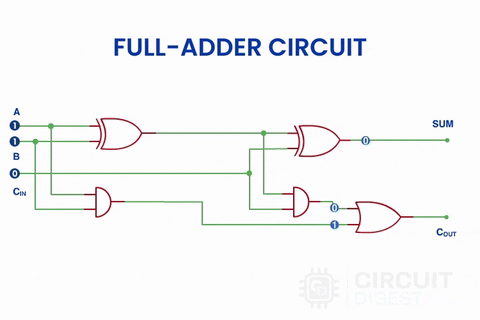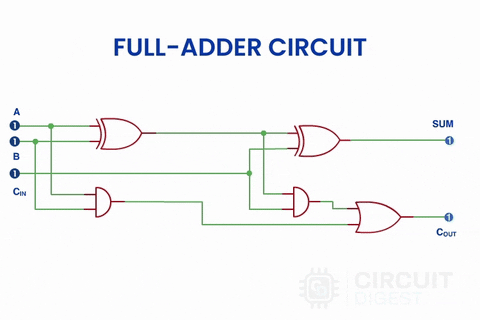
If we see the actual circuit inside the full adder, we will see two Half adders using XOR gate and AND gate with an additional OR gate.

In the above image, instead of the block diagram, actual symbols are shown. In the previous half-adder tutorial, we had seen the truth table of two logic gates which have two input options, XOR and AND gates. Here an extra gate is added in the circuitry, OR gate. And here is a simulation of a full adder circuit with different inputs.
You can learn more about Logic gates here.
Implementation of Full Adder using NAND Gate
We can also construct a full adder circuit using only NAND gates. Here is the circuit diagram for a full adder using only NAND gates.

As you can see the circuit uses 9 NAND gates. And as you may noticed the structure of it is also similar to the previous one. You may also consider them as two half adders with an extra NAND gate. Same as the previous circuit the first section adds the two inputs and the output from the first section is added to the carry in bit using the second stage. The carry from the first stage and the carry from the second stage are then ded to the NAND gate to get the final carry out.
Implementation of Full Adder using NOR Gate
Same as the NAND gates we can also construct a full adder using only the NOR gates. Here is the circuit diagram:

The circuit is exactly similar to the one using the NAND gate, the only difference is that we have used a NOR gate instead of a NAND gate.
Truth Table of Full Adder Circuit:
As Full adder circuit deals with three inputs, the Truth table is also updated with three input columns and two output columns.
| Carry In | Input A | Input B | SUM | Carry Out |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
We can also express the full adder circuit construction in a Boolean expression.
For the case of SUM, We first XOR the A and B input then we again XOR the output with Carry in. So, the Sum is (A XOR B) XOR C.
We can also express it with (A ⊕ B) ⊕ Carry in.
Now, for the Carry out, it is A AND B OR Carry in (A XOR B), which is further represented by A.B + (A ⊕ B).
Cascading Adder Circuits
As of now, we described the construction of a single-bit adder circuit with logic gates. But what if we want to add two more than one-bit numbers?
Here is the advantage of a full adder circuit. We can cascade single-bit full adder circuits and could add two multiple-bit binary numbers. This type of cascaded full adder circuit is called a Ripple Carry Adder circuit.
In the case of the Ripple Carry Adder circuit, the carry-out of each full adder is the Carry in of the next most significant adder circuit. As the Carry bit ripples into the next stage, it is called a Ripple Carry Adder circuit. Carry bit is rippled from the left to right (LSB to MSB).

In the above block diagram, we are adding two three-bit binary numbers. We can see three full adder circuits are cascaded together. Those three full adder circuits produce the final SUM result, which is produced by those three sum outputs from three separate half adder circuits. The Carry out is directly connected to the next significant adder circuit. After the final adder circuit, Carry out provides the final carry out bit.
This type of circuit also has limitations. It will produce unwanted delays when we try to add large numbers. This delay is called the Propagation delay. During the addition of two 32-bit or 64-bit numbers, the Carry out bit, which is the final output’s MSB, waits for the changes in previous logic gates.
To overcome this situation, a very high clock speed is required. However, this problem can be solved using a carry look ahead binary adder circuit where a parallel adder is used to produce carry in bit from the A and B input.
Practical Demonstration of Full Adder Circuit:

We will use a full adder logic chip and add 4 bit binary numbers using it. We will use TTL 4 bit binary adder circuit using IC 74LS283N.
Components used-
4pin dip switches 2 pcs
4pcs Red LEDs
1pc Green LED
8pcs 4.7k resistors
74LS283N
5 pcs 1k resistors
Breadboard
Connecting wires
5V adapter

The above image is of a 74LS283N 4-bit full adder TTL chip with carry look-ahead feature. The circuit diagram to use this 4-bit full adder chip is given below.

Pin 16 and Pin 8 are VCC and Ground respectively, Pin 5, 3, 14 and 12 are the first 4 bits (P) where Pin 5 is the MSB and Pin 12 is the LSB. On the other hand, Pin 6, 2, 15, and 11 are the second 4-bits where Pin 6 is the MSB and Pin 11 is the LSB. Pin 4, 1, 13 and 10 are the SUM output. Pin 4 is the MSB and pin 10 is the LSB when there are no carry out. Pin 9 is the carry out.
4.7k resistors are used in all input pins to provide logic 0 when the DIP switch is in OFF state. With this setup, we can switch from logic 1 (binary bit 1) to logic 0 (binary bit 0) easily. We are using a 5V power supply to power the entire circuit. When the DIP switches are ON, the input pins get shorted with 5V; we used red LEDs to represent the SUM bits and green LED for the carry-out bit.
4-Bit Full Adder TinkerCad Simulation
Let’s simulate the circuit on ThinkerCAD before testing it on the breadboard. Here is the Thinkercad simulation for a 4-bit full adder circuit.
Click on the start simulation button to test the circuit. Now in the simulation, you can change the state of each switch to manipulate the input bits. In the simulation, we have also added LEDs to the input for easy understanding.
The Demonstration Video below shows the real-life circuit for the same, where we have shown adding two 4-bit binary Numbers.





