Most of electronics deals with Tracing Curves, be it the characteristic transfer curve for a feedback loop, a resistor’s straight VI line or a transistor’s collector voltage versus current curve.
These curves give us an intuitive understanding of how a device behaves in a circuit. An analytical approach might involve plugging in discrete voltage and current values into a mathematical formula and graphing the results, commonly with the x axis representing voltage and the y axis representing current.
This approach works, but sometimes it is tedious. And as every electronics hobbyist knows, the behaviour of components in real life can vary (often largely) from the formula describing its operation.
Here we will be using a circuit (Sawtooth waveform) to apply discrete increasing voltage to the component whose VI curve we want to draw and then use a Oscilloscope to view the results.
Simple Curve Tracer
To plot a curve in real time we need to apply successive discrete voltage values to our device under test, so how it can be done?
The solution to our problem is the Sawtooth Waveform.

The Sawtooth waveform rises linearly and goes back to zero periodically. This allows application of a continuously increasing voltage on the device under test and produces a continuous trace on a graph (in this case the oscilloscope).
An oscilloscope in the XY mode is used to ‘read’ the circuit. The X axis is connected to the device under test and the Y axis is connected to the Sawtooth waveform.
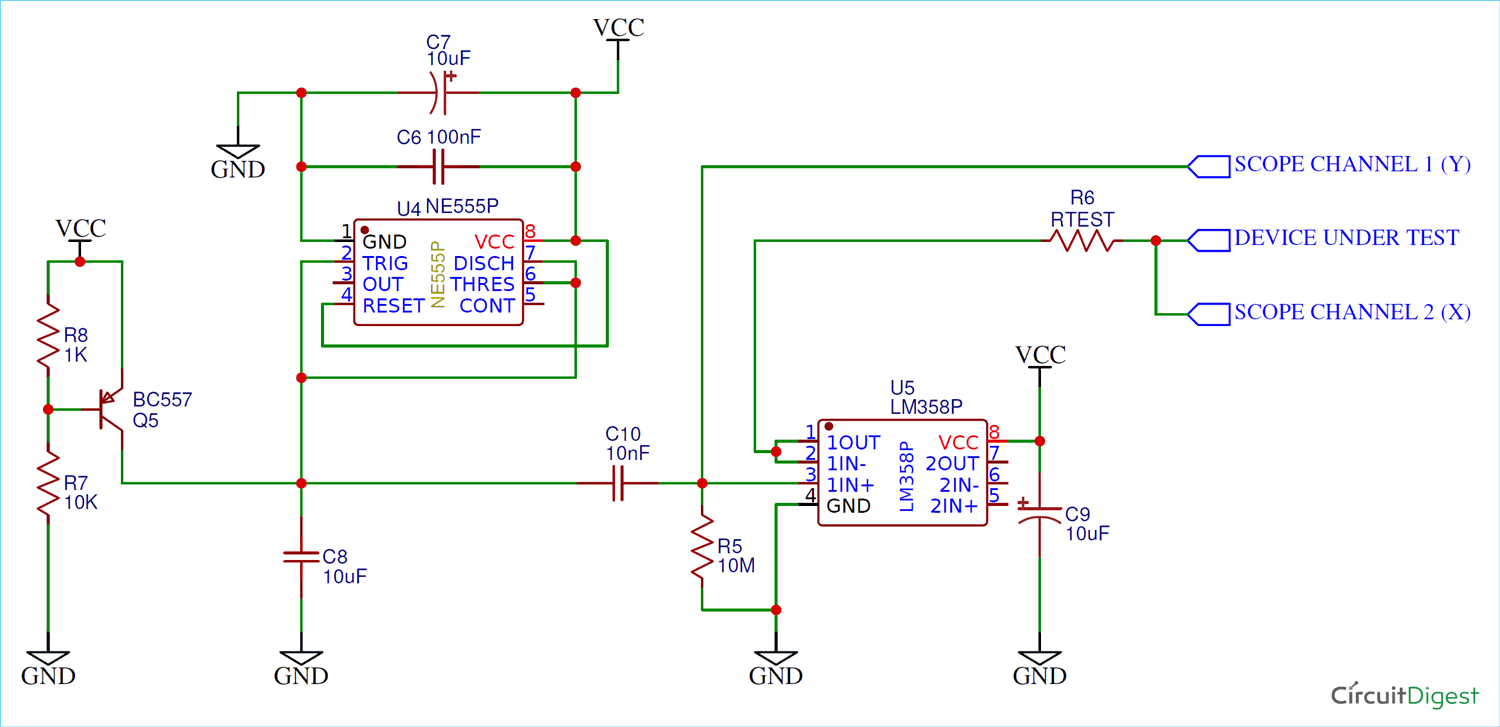
The circuit used here is a simple variation of a curve tracer using common parts like the 555 timer and the LM358 op-amp.
Components Required
1. For the Timer
- 555 timer – any variant
- 10uF electrolytic capacitor (decoupling)
- 100nF ceramic capacitor (decoupling)
- 1K resistor (current source)
- 10K resistor (current source)
- BC557 PNP transistor or equivalent
- 10uF electrolytic capacitor (timing)
2. For the Op-amp Amplifier
- LM358 or comparable opamp
- 10uF electrolytic capacitor (decoupling)
- 10nF ceramic capacitor (AC coupling)
- 10M resistor (AC coupling)
- Test resistor (depends on device under test, usually between 50 Ohms and a few hundred Ohms.)
Circuit Diagram

Working Explanation
1. The 555 Timer
The circuit used here is a simple variation of the classic 555 astable circuit which will work as Sawtooth waveform generator.
Usually the timing resistor is fed through a resistor connected to the power supply, but here it is connected to a (crude) constant current source.
The constant current supply works by providing a fixed base-emitter bias voltage, resulting in a (somewhat) constant collector current. Charging a capacitor using a constant current results in a linear ramp waveform.
This configuration derives the output directly from the capacitor output (which is the sawtooth ramp we’re looking for) and not from pin 3, which provides narrow negative pulses here.
This circuit is clever in the sense that it uses the 555’s internal mechanism to control a constant current source-capacitor ramp generator.

2. The Amplifier
Since the output is derived directly from the capacitor (which is charged from the current source), the current available to power the device under test (DUT) is essentially zero.
To fix this, we’re using the classic LM358 opamp as a voltage (and therefore current) buffer. This somewhat increases the current available to the DUT.
The capacitor Sawtooth waveform oscillates between 1/3 and 2/3 Vcc (555 action), which is unusable in a curve tracer since the voltage does not ramp from zero giving an ‘incomplete’ trace. To fix this the input from the 555 is AC coupled to the buffer input.
The 10M resistor is a bit of black magic –it was found out during testing that if the resistor was not added, the output simply floated to Vcc and stayed there! This is because of the parasitic input capacitance – along with the high input impedance, it forms an integrator! The 10M resistor is enough to discharge this parasitic capacitance but not enough to significantly load the constant current circuit.

How to improve the Curve Tracing Results
Since this circuit involves high frequencies and high impedances, careful construction is needed to prevent unwanted noise and oscillation.
Ample decoupling is recommended. As far as possible, try to avoid breadboarding this circuit and use a PCB or a perfboard instead.
This circuit is very crude and hence temperamental. It is recommended to power this circuit from a variable voltage source. Even a LM317 will work in a pinch. This circuit is most stable at around 7.5V.
Another important thing to consider is the horizontal scale setting on the scope – if too high then all the low frequency noise makes the trace fuzzy and if too low then there’s not enough data to get a ‘complete’ trace. Again, this depends on the power supply setting.
Getting a useable trace requires careful tuning of the oscilloscope timebase setting and input voltage.
If you want useful measurements then a test resistor and the knowledge of opamp output characteristics is required. With a little math good values can be obtained.
How to use Curve Tracer Circuit
There are two simple things to keep in mind – the X axis represents the voltage and the Y axis represents the current.
On an oscilloscope, probing the X axis is quite simple – the voltage is ‘as is’, i.e. corresponds to the volts per division set on the oscilloscope.
The Y or current axis is slightly trickier. We’re not directly measuring the current here, instead we’re measuring the voltage dropped across the test resistor as a result of the current through the circuit.
It is enough if we measure the peak voltage value on the Y axis. In this case, it’s 2V, as seen in previous figure.
So the peak current through the test circuit is
Isweep = Vpeak/Rtest.
This represents the ‘sweep’ current range, from 0 - Isweep.
Depending on the setting, the graph can extend into as many divisions on the screen as that available. So the current per division is simply the peak current divided by the number of divisions the graph extends to, in other words the line parallel to the X axis where the top ‘tip’ of the graph touches.
Curve Tracing for Diode

All the noise and fuzz described above is seen here.
However, the diode curve can clearly be seen, with the ‘knee’ point at 0.7V (note the 500mV per division X scale).
Note that the X axis corresponds exactly with the expected 0.7V, which justifies the ‘as is’ nature of the X axis reading.
The test resistance used here was 1K, so the current range was from 0mA – 2mA. Here the graph does not exceed two divisions (approximately), so a rough scale would be 1mA/division.
Curve Tracing for Resistor

Resistors are electrically the simplest devices, with a linear VI curve, a.k.a Ohm’s law, R = V/I. It is obvious that low value resistors have steep slopes (higher I for given V) and high value resistors have more gentle slopes (less I for given V).
The test resistance here was 100 Ohms, so the current range was 0mA – 20mA. Since the graph extends to 2.5 divisions, the current per division is 8mA.
The current rises 16mA for a volt, so the resistance is 1V/16mA = 62 Ohms, which is appropriate since a 100 Ohm pot was the DUT.
Curve Tracing for Transistor
Since the transistor is a three terminal device, the number of measurements that can be made is quite large, however, only a few of those measurements find common use, one of them being the dependence of collector voltage on base current (both referenced to ground, of course) at a constant collector current.
Using our curve tracer this should be an easy task. The base is hooked up to a constant bias and the X axis to the collector. The test resistance provides the ‘constant’ current.
The resultant trace should look something like this:

IB Vs VCE
Note that the graph shown above is a log scale, remember that the oscilloscope is linear by default.
So Curve tracers are devices that produce VI traces for simple components and help gain an intuitive understanding of component characteristics.