Aside from safety and reliability, several other goals including efficiency should be pursued in the design and implementation of electrical systems. One of the measures of efficiency in an electrical system is the efficiency with which the system transforms the energy it receives into useful work. This efficiency is indicated by a component of electrical systems known as the Power Factor. The power factor indicates how much power is actually being used to perform useful work by a load and how much power it is “wasting”. As trivial as its name sounds, it is one of the major factors behind high electricity bills and power failures.
To be able to properly describe power factor and its practical significance, it is important to refresh your memory about the different types of electrical loads and components of Power that exist.
From basic electricity classes, electrical loads are typically of two types;
- Resistive Loads
- Reactive Loads
1. Resistive Loads
Resistive loads, as the name implies these loads are made up of purely resistive elements. For this kind of loads (considering ideal conditions), all the power supplied to it are dissipated for work due to the fact that the current is in phase with the voltage. A good example of resistive loads includes incandescent light bulbs and batteries.

The power component associated with resistive loads is referred to as Actual Power. This Actual Power is also sometimes called as Working Power, True Power or Real Power. If you are new to AC power and feel confused with all these waveforms, then it is recommended to read about the basics of AC to understand how AC power works.
2. Reactive loads
Reactive loads on the other hand, are a little bit more complex. While they cause a drop in voltage and draw current from the source, they dissipate no useful power as such because the power they draw from supply does no work. This is dues to the nature of the Reactive Loads.
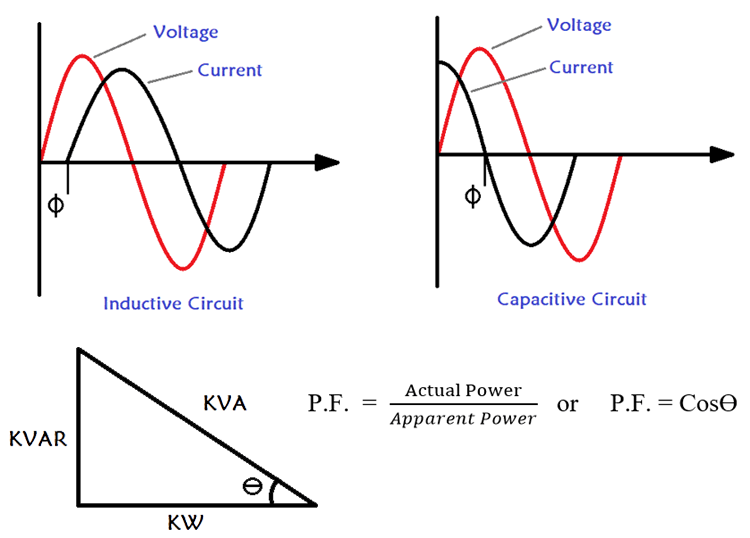
Reactive loads can either be capacitive or Inductive. In inductive loads, the power drawn is used up in setting up magnetic flux without any direct work performed while for capacitive loads, the power is used in charging the capacitor and not directly producing work. The power thus dissipated in reactive loads is referred to as Reactive power. Reactive loads are characterized by the current leading (Capacitive loads) or lagging (Inductive loads) behind the voltage, as such, a phase difference usually exists between the current and the voltage.


The above two graphs represents an Inductive and Capacitive load where the Power factor is lagging and leading respectively. The variations in these two types of load leads to the existence of three power components in electrical systems, namely;
- Actual Power
- Reactive Power
- Apparent Power
This is the power associated with resistive loads. It is the power component dissipated to the performance of actual work in electrical systems. From heating to lighting, etc., It is expressed in Watts (W) (along with its multipliers, kilo, Mega, etc.) and symbolically represented by the letter P.
This is the power associated with reactive loads. As a result of the delay between voltage and current in reactive loads, the energy drawn in reactive, (either capacitive or inductive) produces no work. It is referred to as Reactive power and its unit is Volt-Ampere Reactive (VAR).
Typical electrical systems comprise of both resistive and inductive loads, think about your light bulbs and heaters for resistive loads, and equipment with motors, compressors, etc as inductive loads. Thus in an electrical system, Total Power is a combination of the actual and reactive power components, this total power is also called as Apparent Power.
The apparent power is given by the sum of the Actual power and reactive power. Its unit is volt-amps (VA) and represented mathematically by the equation;
Apparent Power = Actual Power + Reactive power
In Ideal situations, the actual power dissipated in an electrical system is usually greater than the reactive power. The below image shows the vector diagram drawn using the three Power Components

This vector diagram can be transformed into the power triangle as shown below.

The Power factor can be calculated by obtaining the angle theta (ϴ) shown above. Here theta is the angle between the Real Power and Apparent Power. Then, following the cosine rule (Adjacent over hypotenuse), the power factor can be estimated as the ratio of actual power to the apparent power. The formulae to calculate Power Factor is given below
P.F. = Actual Power / Apparent Power or P.F. = Cosϴ
Putting this side by side with the equation for determining apparent power, it's easy to see that an increase in reactive power (presence of a high number of reactive loads), leads to an increase in apparent power and a larger value for angle ϴ, which ultimately results in a low power factor when its cosine (cos ϴ) is obtained. On the flip side, reduction in reactive loads (reactive power) leads to an increased power factor, indicating high efficiency in systems with less reactive loads and vice versa. The value of Power Factor will always be between the value of 0 and 1, the closer it gets to one the higher will be the efficiency of the system. In India the ideal power factor value is considered to be 0.8. The value of power factor has no unit.
Importance of Power Factor
If the value of power factor is low it means, energy from mains is being wasted since a huge chunk of it is not being used for meaningful work. This is because the load here consumes more reactive power compared to the real power. This places a strain on the supply system causing an overload on distribution system as both the real power required by the load and the reactive power used to satisfy reactive loads will be drawn from the system.
This strain and “wastage” typically leads to huge electricity bills for consumers(especially industrial consumers) as utility companies calculate consumption in terms of apparent power, as such, they end up paying for power which was not used to achieve any “meaningful” work. Some companies also fine their consumers if they draw more reactive power since it causes an overload on the system. This fine is imposed so as to reduce low power factor causing loads being used in industries.
Even in situations where the power is being provided by the company’s generators, money is wasted on bigger generators, larger sized cables, etc required to provide power when a good number of it is just going to be wasted. To better understand this, consider the below example
A factory operating a 70kW load could be powered successfully by a Generator/ Transformer and cables rated for 70 kVA if the factory is operating with a power factor of 1. But, if the power factor drops down to 0.6 then even with the same load of 70KW, a larger generator or transformer rated for 116.67 kVA (70/0.6) will be required, as the generator/transformer will have to supply the additional power for the reactive load. Asides this heavy rise in power requirements, the size of the cables used would also need to be increased, leading to a significant increase in equipment cost and increased power losses as a result of the resistance along the conductors. The punishment for this goes beyond high electricity bills in some countries, as companies with poor power factor usually get fined huge sums to encourage rectification.
Improving the Power Factor
With all that has been said, you will agree with me that it makes more economic sense to rectify the poor power factor than to keep paying huge electricity bills, especially for large industries. It is also estimated that over 40% on electricity bills can be saved in huge industries and manufacturing plants if the power factor is corrected and kept low.
Aside from the reduction in cost for consumers, running an efficient system contributes to the overall reliability and efficiency of the power grid, as utility companies are able to reduce losses in lines and cost of maintenance while also experiencing a reduction in the amount of transformers and similar support infrastructure required for their operations.
Calculating Power Factor for your Load
The first step to correcting the power factor is determining the power factor for your load. This can be done by;
1. Calculating the reactive power using the reactance details of the load
2. Determining the real power being dissipated by the load and combining it with the apparent power to obtain the power factor.
3. The use of the power factor meter.

The power factor meter is mostly used as it helps to easily obtain the power factor in large system setups, where determining the reactance details of the load and the real power dissipated, may be a difficult route.
With the power factor known you can then proceed to correct it, adjusting it as close as possible to 1.nThe Recommended power factor by electricity supply companies, is usually between 0.8 and 1 and this can only be achieved if you are running an almost purely resistive load or the inductive reactance (load) in the system is equal to the capacitance reactance as they both will cancel each other out.
Due to the fact that the use of inductive loads is a more common cause for low power factor, especially in industrial settings (due to the use of heavy motors etc), one of the simplest methods of correcting the power factor is by canceling out the inductive reactance through the use of correction capacitors which introduce capacitive reactance in the system.
Power factor correction capacitors act as a reactive current generator, countering / offsetting the power being “wasted” by inductive loads. However, careful design consideration needs to be made when inserting these capacitors in setups to ensure smooth operation with equipment like variable speed drives and an effective balance with cost. Depending on the facility, and load distribution, the design could comprise of fixed value capacitors installed at inductive load points or automatic correction capacitor banks installed on the bus bars of distribution panels for a centralized correction which is usually more cost effective in large systems.
The use of power factor correction capacitors in setups has its downsides, especially when the right capacitors are not used or the system is not properly designed. The use of the capacitors could produce some brief period of “over-voltage”, when turned on, which could affect proper functioning of equipment like variable speed drives, causing them to go off intermittently or blowing up the fuses on some of the capacitors. It could, however, be solved by trying to make adjustments to the switching control sequence, in the case of speed drives or eliminating harmonic currents in the case of fuses.
Unity Power Factor and why it’s not practical
When the value of your Power factor is equal to 1, then the power factor is said to be unity power factor. It might be tempting to obtain the optimal power factor of 1, but it is almost impossible to attain it due to the fact that no system is truly ideal. In the sense no load is purely resistive, capacitive or inductive. Every load comprises of some of elements of the other no matter how small, as such typical realizable power factor range is usually up to 0.9/0.95. We have already learnt about these parasitic properties of the RLC elements in our ESR and ESL with Capacitors articles.
Power factor is a determinant of how well you are using energy and how much you pay in electricity bills (especially for industries). By extension, it is major contributor to operational cost and could be that factor behind reduced profit margins that you have not been paying attention to. Improving the power factor of your electrical system could help reduce electricity bills and ensure performance is maximized.





