These AC circuits series has taken us on a journey which has seen us discuss what AC really is all about, how its generated, some histories, concepts behind AC, its waveform, characteristics and some properties. Today we will be going over some terms and quantities associated with the Alternating Current.
Peak Value of An AC Waveform
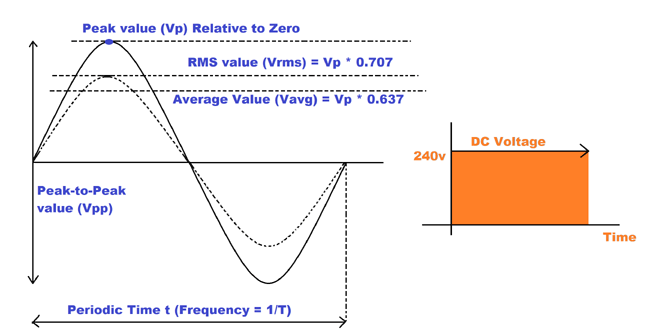
One of the key properties of an AC waveform, asides frequency and period, is the Amplitude which represents the maximum value of an alternating waveform or as better known, the peak value.
Peak as the word denotes, is the highest attained value by an alternating current’s (or voltage) waveform during an half cycle of the waveform measured from the baseline starting point at zero. This gives us one of the major difference between AC and DC as DC based signals are steady state signals, thus they maintain a constant amplitude which is always equal to the magnitude of the DC current or voltage. In Pure sine waves, the Peak value is always the same for both the positive and negative half cycles that makes a complete cycle (+Vp = -Vp), but this doesn’t hold true for other none sinusoidal waveforms used in representing the alternating current, as different half cycles tend to have different peak values.
Instantaneous Values of Voltage and Current
The Instantaneous value of an Alternating voltage or current is the value of the current or voltage at a particular instant of time during the cycle of the waveform.
Consider the Image below.
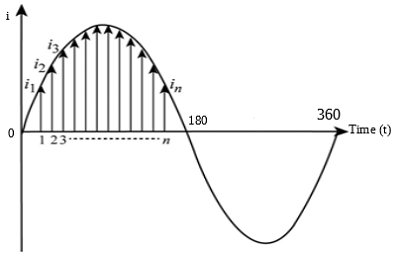
The Instantaneous value of voltage is given by the equation;
V = Vpsin2πFt
Where Vp = value of the peak voltage
The instantaneous value of current is also obtained by a similar expression
I = Ipsin2πFt
Average Value of an AC Waveform
The average value or mean value of an alternating current is the average of all instantaneous values during an half cycle. It is the ratio of all instantaneous values to the number of instantaneous values selected during a half cycle.
The average value of an AC waveform is giving by the equation;
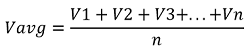
Where V1...Vn is the instantaneous value of voltage during the half cycle.
The average value is also given by the equation;
Vavg = 0.637 *Vp
Where Vp is the maximum/ Peak value of voltage in that cycle.
This same equation also holds true for current and all we have to do is swap Voltage in the equation for Current.
The average value of an AC wave is only measured during a half cycle for a singular reason; when measured over a full cycle, the resultant average value is always equal to zero because the average value of the positive half cycle will cancel out that of the negative half cycle and as a result the expression based on the equation given above will evaluate to zero.
Root Mean Square (RMS) Value of an AC waveform
The square root of the sum of the squares of the mean values of an alternating current or voltage is referred to as the root mean square or RMS value of the voltage or current. It is given by the relation;
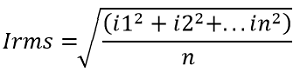
Where i1 to in represent instantaneous values of current.
Or
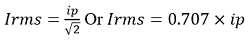
Where Ip is the maximum or peak current.
The same set of equations hold for voltage and we just need to replace current with voltage in the equations.
It is advisable that the RMS values of voltage and current are used as much as possible when doing alternating current related calculations except for when performing average power-related calculations. The reason for this is the fact that most measuring instruments (multi-meters) used for measuring Alternating voltage and current give their outputs as rms values. Thus as much as possible to avoid errors, one should only use Vp to find Ip and Vrms to find Irms and vice versa as this quantities are completely different from one another.
Form Factor
One other quantity associated with an Alternating current that we need to look at is the form factor.
The form factor is a parameter used in describing AC waveforms and is giving by the ratio between the RMS value of the alternating quantity and the average value.
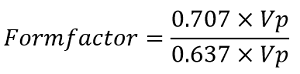
Where Vp is the peak or maximum voltage.
One of the ways of determining if a sine wave is pure is via the form factor, which for a pure sine wave will always give a value of 1.11.
We can also Derive Irms from above equation like:
Form Factor = (0.707 x Vp) / (0.637 x Vp) 1.11 = Irms / Vavg Irms = 1.11 x Vavg
One other application of form factors is found in digital multimeters used in measuring Alternating current or voltage. Most of these meters are generally scaled to display the RMS value of sine waves which they are designed to obtain by calculating the average value and multiplying by the form factor of a sinusoid (1.11) since it can be a little bit difficult to digitally calculate the rms values. Thus at times, for AC waveforms which are not pure sinusoidal, the reading from a multimeter may be a little bit inaccurate.
Crest Factor
The last quantity associated with the alternating current that we will be talking about in this article is the Crest Factor.
The crest factor is the ratio of the peak value of an alternating current or voltage to the root mean square of the waveform. Mathematically, it is given by the equation;
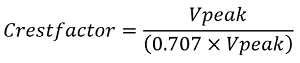
Where Vpeak is the maximum amplitude of the waveform.
For a pure sine wave, similar to the form factor, the crest factor is always fixed at 1.414.
We can also Derive Irms from above equation like:
1.414 = Vpeak / (0.707 x Vpeak) Vrms = V peak / 1.414 Vrms = 0.707 x Vpeak
The crest factor is majorly an indication of how high the peaks of an alternating quantity are. In direct current, for instance, the crest factor is always equal to 1 which is an indication of the lack of peaks in the waveform of a Direct current.
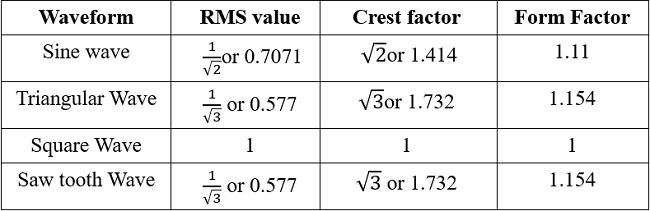
To serve as a sort of the key point below is a table showing the form factors and crest factors of different type of waveforms used in representing AC waveforms.






Great explanation and formulaes