Hello everyone,
In connection with the development of a program for Boolean minimization, think e.g. to Quine-McCluskey, I need examples and their correct solution so that I can check my program for correct operation. The number of variables may not exceed 20, and preferably between 4 and 10. The examples may be presented in this form (see the truth table below) : CD'+A'BC'+AC'D (C AND (NOT D) OR (NOT A) AND B AND (NOT C) OR A AND (NOT C) AND D). I would like to receive a response from you. Kind regards, Karel.
i A B C D X
0 0 0 0 0 0
1 0 0 0 1 0
2 0 0 1 0 1
3 0 0 1 1 0
4 0 1 0 0 1
5 0 1 0 1 1
6 0 1 1 0 1
7 0 1 1 1 0
8 1 0 0 0 0
9 1 0 0 1 1
10 1 0 1 0 1
11 1 0 1 1 0
12 1 1 0 0 0
13 1 1 0 1 1
14 1 1 1 0 1
15 1 1 1 1 0
This has to do with digital electronics. Especially for minimizing AND & OR gate circuits. If you're not familiar with this, it won't mean anything to you. Sincerely, Karel.

Representation of Boolean Functions” every boolean function can be expressed as a sum of minterms or a product of maxterms. Since the number of literals in such an expression is usually high, and the complexity of the digital logic gates that implement a Boolean function is directly related to the complexity of the algebraic expression from which the function is implemented, it is preferable to have the most simplified form of the algebraic expression.
The process of simplifying the algebraic expression of a boolean function is called minimization. Minimization is important since it reduces the cost and complexity of the associated circuit.
For example, the function F=x^\prime y^\prime z + x^\prime yz + xy^\prime can be minimized to F=x^\prime z + xy^\prime. The circuits associated with above expressions is –
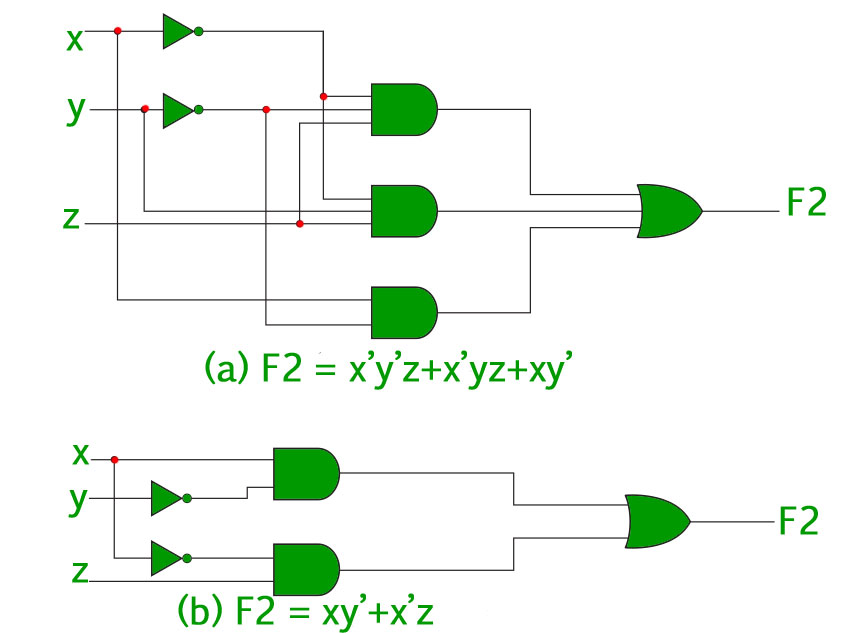
It is clear from the above image that the minimized version of the expression takes a less number of logic gates and also reduces the complexity of the circuit substantially. Minimization is hence important to find the most economic equivalent representation of a boolean function.
Minimization can be done using Algebraic Manipulation or K-Map method. Each method has it’s own merits and demerits.

So how did you manage to solve the problem? I ask because the end result is interesting


Karel Lucas
PermalinkPart of it has been dropped due to an error. It should have said:
The examples may be presented in this form (see truth table below): X {A, B, C, D} = Σ {2,4,5,6,9,10,13,14}, with the solution: CD '+ A'BC' + AC'D (C AND (NOT D) OR (NOT A) AND B AND (NOT C) OR A AND (NOT C) AND D).
- Log in or register to post comments
Joined August 21, 2020 2Friday at 04:02 AM