A capacitor is one of the most used electronic components. It has the ability to store energy inside it, in the form of an electrical charge producing a static voltage (potential difference) across its plates. Simply, a capacitor is similar to a small rechargeable battery. A capacitor is just a combination of two conductive or metal plates places parallel, and are electrically separated by good insulating layer (also called Dielectric) made up of waxed paper, mica, ceramic, plastic and etc.
There are many applications of a capacitor in electronics, some of them are listed below:
- Energy Storage
- Power Conditioning
- Power factor Correction
- Filtration
- Oscillators
Now, the point is how a capacitor work? When you connect power supply to the capacitor it blocks the DC current due to insulating layer, and allow a voltage to be present across the plates in the form of electrical charge. So, you know how a capacitor works and what are its uses or application, but you have to learn that how to use a capacitor in electronic circuits.
How to Connect a Capacitor in Electronic Circuit?
Here, we are going to demonstrate you the connections of a capacitor and effect due to it with examples.
- Capacitor in Series
- Capacitor in Parallel
- Capacitor in AC Circuit
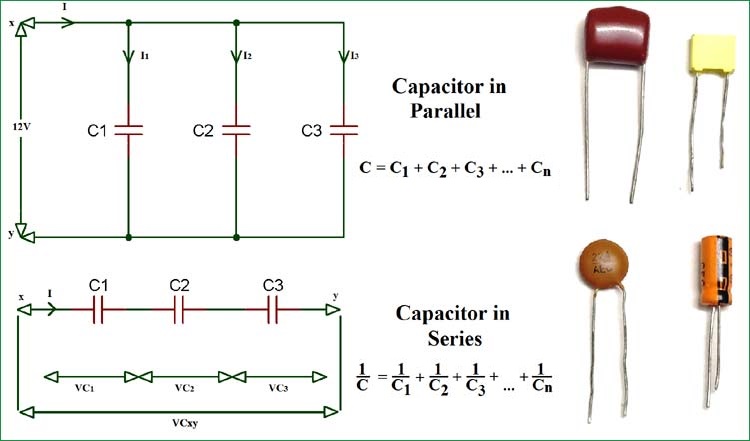
Capacitor in Series Circuit
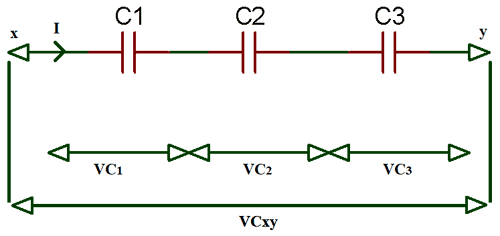
In a circuit, when you connect capacitors in series as shown in the above image, the total capacitance is decreased. The current through capacitors in series is equal (i.e. iT = i1 = i2 = i3= in). Hence, the charge stored by the capacitors is also the same (i.e. QT = Q1 = Q2 = Q3), because charge stored by a plate of any capacitor comes from the plate of adjacent capacitor in the circuit.
By applying Kirchhoff’s Voltage Law (KVL) in the circuit, we have
VT = VC1 + VC2 + VC3 … equation (1)
As we know,
Q = CV So, V = Q / C
Where, VC1 = Q / C1; VC2 = Q / C2; VC3 = Q / C3
Now, on putting the above values in the equation (1)
(1 / CT) = (1 / C1) + (1 / C2) + (1 / C3)
For n number of capacitor in series the equation will be
(1 / CT) = (1 / C1) + (1 / C2) + (1 / C3) + …. + (1 / Cn)
Hence, the above equation is the Series Capacitors Equation.
Where, CT = Total capacitance of the circuit
C1…n = Capacitors capacitance
Capacitance Equation for two special cases is determined below:
Case I: if there are two capacitor in series, with different value the capacitance will be expressed as:
(1 / CT) = (C1 + C2) / (C1 * C2) Or, CT = (C1 * C2) / (C1 + C2) … equation (2)
Case II: if there are two capacitor in series, with same value the capacitance will be expressed as:
(1 / CT) = 2C / C2 = 2 / C Or, CT = C / 2
Example for Series Capacitor Circuit:
Now, in the below example we will show you how to calculate total capacitance and individual rms voltage drop across each capacitor.
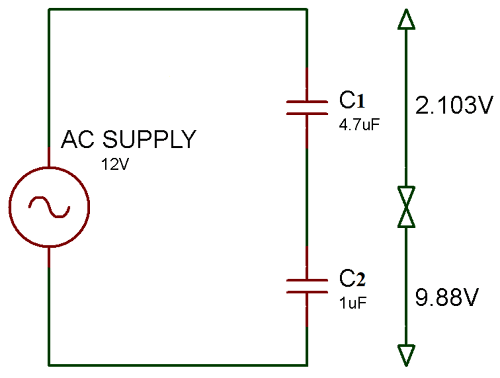
As, per the above circuit diagram there are two capacitors connected in series with different values. So, the voltage drop across the capacitors is also unequal. If we connect two capacitors with same value the voltage drop is also same.
Now, for the total value of capacitance we will use the formula from equation (2)
So, CT = (C1 * C2) / (C1 + C2) Here, C1 = 4.7uf and C2 = 1uf CT = (4.7uf * 1uf) / (4.7uf + 1uf) CT = 4.7uf / 5.7uf CT = 0.824uf
Now, voltage drop across the capacitor C1 is:
VC1 = (CT / C1) * VT VC1 = (0.824uf / 4.7uf) * 12 VC1 = 2.103V
Now, voltage drop across the capacitor C2 is:
VC2 = (CT / C2) * VT VC2 = (0.824uf / 1uf) * 12 VC2 = 9.88V
Capacitor in Parallel Circuit
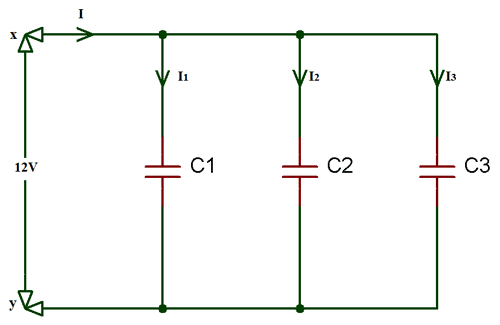
When you connect capacitors in parallel, then the total capacitance will be equal to the sum of all the capacitors capacitance. Because the top plate of all the capacitors are connected together and the bottom plate also. So, by touching each other the effective plate area is also increased. Therefore, the capacitance is proportional to the ratio of Area and distance.
By applying Kirchhoff’s Current Law (KCL) in the above circuit,
iT = i1 +i2 + i3
As we know current through a capacitor is expressed as;
i = C (dV / dt) So, iT = C1 (dV / dt) + C2 (dV / dt) + C3 (dV / dt) And, iT = (C1 + C2 + C3)* (dV / dt) iT = CT (dV / dt) … equation (3)
From equation (3), the Parallel Capacitance equation is:
CT = C1 + C2 + C3
For n number of capacitors connected in parallel the above equation is expressed as:
CT = C1 + C2 + C3 + … + Cn
Example for Parallel Capacitor Circuit
In the below circuit diagram, there are three capacitors connected in parallel. As these capacitors are connected in parallel the equivalent or total capacitance will be equal to the sum of the individual capacitance.
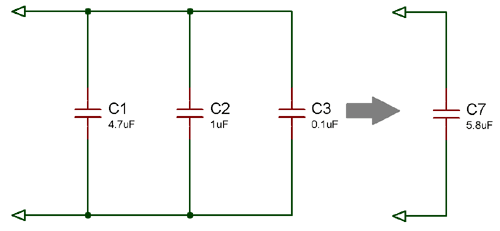
CT = C1 + C2 + C3 Where, C1 = 4.7uf; C2 = 1uf and C3 = 0.1uf So, CT = (4.7 +1 + 0.1)uf CT = 5.8uf
Capacitor in AC circuits
When a capacitor is connected to DC supply, then the capacitor starts charging slowly. And, when the charging current voltage of a capacitor is equal to the supply voltage it’s said to fully charged condition. Here, in this condition the capacitor works as an energy source as long as voltage is applied. Also, capacitors do not allow the current to pass through it after it get fully charged.
Whenever, AC voltage is supplied to the capacitor as shown in above purely capacitive circuit. Then the capacitor charges and discharges continuously to every new voltage level (charges on positive voltage level and discharge on negative voltage level). The capacitor’s capacitance in AC circuits depends on the frequency of input voltage supplied to the circuit. The current is directly proportional to the rate of change of voltage applied to the circuit.
i = dQ / dt = C (dV / dt)
Phasor diagram for Capacitor in AC Circuit
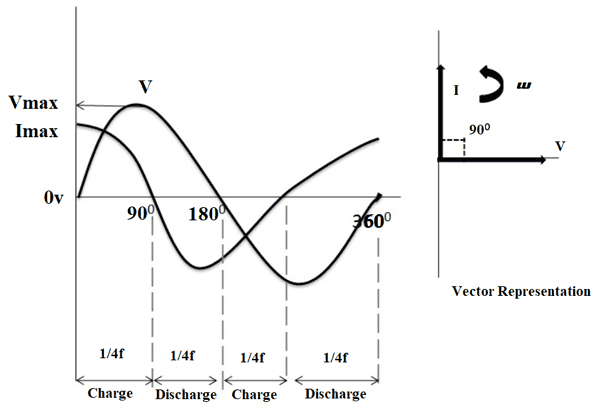
As you see the phasor diagram for AC capacitor in the below image, current and voltage are represent in sine wave. On observing, at 0⁰ the charging current is at its peak value because of the voltage increasing in positive direction steadily.
Now, at 90⁰ there is no current flow through the capacitor because the supply voltage reaches to the maximum value. At 180⁰ the voltage start decreasing slowly to zero and current reach to maximum value in negative direction. And, again the charging reaches to its peak value at 360⁰, because of supply voltage is at its minimum value.
Therefore, from the above waveform we can observe that the current is leading the voltage by 90⁰. So, we can say that the AC voltage lags the current by 90⁰ in an ideal capacitor circuit.
Capacitor Reactance (Xc) in AC Circuit
Consider the above circuit diagram, as we know AC input voltage is expressed as,
V = VmSinwt
And, capacitor charge Q = CV,
So, Q = CVmSinwt
And, current through a capacitor, i = dQ / dt
So,
i = d (CVmSinwt) / dt i = C * d (VmSinwt) / dt i = C*VmCoswt *w i = w*C*VmSin(wt + π/2) at, wt = 0 sin(wt + π/2) = 1 hence, im = wCVm Vm / im = 1 / wC
As we know, w = 2πf
So,
Capacitive Reactance (Xc) = Vm / im = 1 / 2πfC
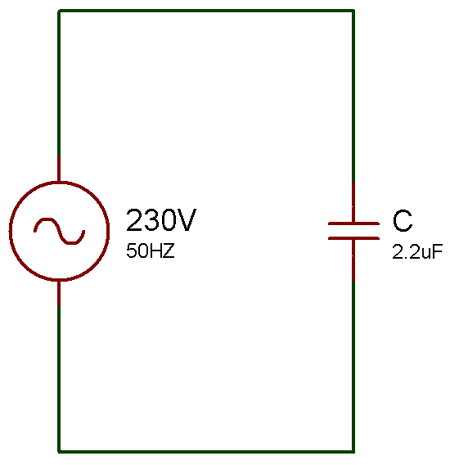
Example for Capacitive Reactance in AC Circuit
diagram
Let’s, consider the value of C = 2.2uf and the supply voltage V = 230V, 50Hz
Now, the Capacitive Reactance (Xc) = Vm / im = 1 / 2πfC Here, C = 2.2uf, and f = 50Hz So, Xc = 1 / 2*3.1414*50*2.2*10-6 Xc = 1446.86 ohm






Pls correct the equation in the introduction image. They are interchanged.
Actualy parallel capacitor value is equal to C= C1+C2+C3